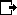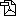1S’il existe des écrivains de science-fiction, on parle moins volontiers d’artistes de science-fiction. Ces derniers existent pourtant. Ils ne se contentent pas d’illustrer des histoires et des mondes de science-fiction, comme d’autres donnent forme à la belle nature ou aux chimères de nos rêves ; ils produisent quelque chose de plus étonnant : de l’art-fiction, ou plutôt des fictions d’art ajustées aux questions de la science. Les arts visuels ou plastiques, et singulièrement l’art dit « contemporain », parviennent à inventer sous un régime de fiction (ou de « comme si ») des configurations d’expérience qui, tout en puisant dans leurs ressources propres (peinture, sculpture, mais aussi « projet », « installation » ou « dispositif »), entretiennent avec les fictions et les modèles scientifiques un rapport parallèle à celui que la littérature de science-fiction a construit pour son compte, et depuis longtemps, avec l’univers des sciences et des techniques.

2C’est donc vers la littérature et les arts qu’il faut se tourner, non pour savoir où est le virtuel, ni à quoi il ressemble, questions qui cherchent encore à ressaisir le virtuel dans les catégories de la réalité, mais plutôt quelle est sa « tenue », ou sa « consistance ». Il y va alors d’autre chose que d’atmosphères et de textures (l’imaginaire cinématographique du virtuel inspiré des jeux vidéo s’en tient trop souvent à cela). Si le virtuel ne se réduit pas à un décor, s’il relève, non pas des mondes possibles, mais d’un régime particulier du réel lui-même (celui des états virtuels, distincts des états actuels sur le terrain même du réel), il y a lieu de se demander dans quelles dimensions il se déploie, mais aussi quel type de connexité lui convient, et enfin comment il se raccorde à notre espace-temps familier. Questions de topologie, plutôt que d’ontologie. Questions  inséparables, en tout cas, du souci de dégager, sous le régime de la fiction, les formes d’une expérience sensible. Marcel Duchamp est en ce sens un artiste de science-fiction, en tout cas un des producteurs d’art-fiction les plus singuliers du siècle passé. Il propose, à sa manière, une enquête d’inspiration topologique sur les états virtuels et leur mode d’accès.

Le cas Duchamp

3Comme beaucoup de ses confrères, Duchamp était grand amateur de vulgarisation scientifique romancée (le voyage au pays de la quatrième dimension de Gaston de Pawlowski, publié en 1912, est plus loufoque encore que le drolatique Flatland d’Edwin A. Abbott1). Mais il était aussi un lecteur assidu de La revue des idées et de La nature. Il y croisait les noms de Maxwell, de Kelvin, de Röntgen, de Rutherford, ou encore de Poincaré dont il avait longuement pratiqué La science et l’hypothèse (1902). Radioactivité et thermodynamique, mouvement brownien et rayons-X, éther et électrons, géométries non euclidiennes et quatrième dimension, étaient dans l’air du temps. Plus obstiné que d’autres, l’inventeur des « ready made » n’hésitait pas à se plonger également dans des manuels de géométrie comme le Traité élémentaire de géométrie à quatre dimensions de Jouffret (1903). Que cherchait-il en s’installant ainsi à l’intersection de l’art et de la science ? Un simple divertissement espiègle, à la manière d’Alfred Jarry et de sa pataphysique ? La mise en œuvre plastique de concepts scientifiques ? La question divise les experts. Mais elle est peut-être, en l’occurrence, mal posée. Car l’important n’est pas de savoir si Duchamp fait de la géométrie (bien sûr que non…), mais ce qu’il fait de la géométrie lorsqu’il fait de l’art. Or son intérêt singulier pour les questions géométriques va bien au-delà de la « science amusante ». Quelques pièces en témoignent.

4Les « stoppages étalons » (1913-1914), obtenus en laissant choir un fil d’un mètre de longueur et en reportant leur forme au sol sur des règles de bois, suggèrent la mesure d’espaces à courbure variable. Ils donnent aussi une illustration tangible d’une thèse philosophique défendue par le mathématicien Poincaré, celle du caractère conventionnel des axiomes géométriques, comparable selon lui au caractère conventionnel des unités de mesure. Mais c’est surtout dans Le grand verre (1915-1923), également connu sous le titre énigmatique de La mariée mise à nu par ses célibataires même, que se déploient les ressources d’invention que Duchamp puise dans les mathématiques. Cette œuvre aujourd’hui exposée à Philadelphie fut, pendant quelques années, son laboratoire de recherche. Elle totalise un parcours, et témoigne peut-être, à sa manière, d’une difficulté que Duchamp n’est parvenu à résoudre qu’en principe, sans aboutir à une élaboration plastique satisfaisante à ses yeux.

5Pour s’en rendre compte, il faut prendre le Grand verre avec l’ensemble de ses notes et schémas préparatoires (les diverses « boîtes », dont l’artiste disait qu’elles offraient « une sorte d’explication diagrammatique et programmatique de ce qu’on peut voir sur le Verre »). Car il faut bien avouer que l’œuvre par elle-même est assez opaque, et ne se livre pas facilement : ce n’est pas pour rien que Duchamp est aussi souvent mentionné comme le père de l’« art conceptuel ». Le Grand verre, si l’on suit son auteur, doit être abordé comme la projection tridimensionnelle, elle-même reportée en deux dimensions sur un double panneau de verre, d’une scène invisible à quatre dimensions. Mais l’essentiel n’est pas là. Duchamp ne se contente pas d’invoquer la quatrième dimension comme une forme d’hyperréalité qui outrepasserait les bornes de notre sensibilité ou de notre imagination visuelle et tactile, et dont l’artiste ne pourrait recueillir que des images diffractées dans le visible ; il ne la situe pas aux confins de l’« art rétinien », comme une sorte de point de fuite imaginaire de la représentation perspective. Exploiter les ressources de la géométrie quadridimensionnelle pour imposer de nouveaux modes de figuration, c’est ce que fit Picasso avec la perspective éclatée du Portrait d’Ambroise Vollard (1910), et de façon plus radicale encore, avec le Portrait d’Henry Kahnweiler (1910). Mais Duchamp donne forme à un problème plus fondamental : il veut faire saisir la manière dont les différentes dimensions (et singulièrement la troisième et la quatrième) s’articulent les unes aux autres. Pour cela, il se propose de redéfinir la virtualité elle-même à partir de la quatrième dimension, en cherchant à construire le dispositif qui la révélera pour ainsi dire de l’intérieur, dans l’élément même du sensible.

« Virtualité comme quatrième dimension : non pas la Réalité sous l’apparence sensorielle, mais la représentation virtuelle d’un volume (analogue à sa réflexion dans un miroir). »2

6Cet énoncé un peu cryptique prend tout son sens si on prend la peine de le rapporter aux remarques qui l’encadrent. Il suggère un programme : traiter la quatrième dimension de manière intrinsèque, non analogique, en l’adossant à une définition topologique de la dimension. L’idée, si l’on développe jusqu’au bout l’intuition de Duchamp, est à peu près la suivante : au lieu de saisir la quatrième dimension par les bords, c’est-à-dire par les frêles profils qu’elle nous présente en trois dimensions, essayons plutôt de nous installer en elle d’un seul coup, par une sorte de saut de l’esprit. Ce saut, le dispositif entier du Grand verre, avec ses multiples programmes et diagrammes, est chargé d’en établir la possibilité, et même la nécessité.

7Une formulation un peu différente de la même exigence nous conduirait à insister sur le caractère intrinsèque de la démarche : si la quatrième dimension peut être ressaisie à partir de la troisième (comment faire autrement ?), ce ne sera pas comme une limite extérieure, mais à la manière d’une dimension évanouissante, sur le point de se résorber à la « surface » de notre espace habituel. La réalité serait ainsi le dépôt, le résidu (plutôt que la projection) de formes quadridimensionnelles qu’un esprit supérieur pourrait déplier dans une dimension supplémentaire. Et la virtualité serait justement la pellicule évanescente, proprement « inframince », qui nous sépare de cette autre dimension. Ressaisie à travers l’expérience du virtuel, la quatrième dimension n’est pas reléguée aux confins de la réalité ou dans l’on ne sait quel fond sans fond ; elle ne doit pas être cherchée ailleurs qu’à sa surface, ou dans ses franges.

8En cherchant à donner forme à cette intuition étrange, Duchamp fait écho à l’un des gestes les plus puissants des mathématiques du xix^e siècle : la caractérisation intrinsèque de la courbure des surfaces, dont Gauss a livré la clé. Mais il touche simultanément à une caractérisation topologique de la dimension qui nous renvoie directement à Poincaré. Ces résonances suggèrent une voie féconde pour toute une gamme d’expérimentations science-fictionnelles de l’espace, dont la littérature a déjà donné quelques exemples frappants. Les observations qui suivent se contenteront d’expliciter les termes du projet duchampien, sans prétendre rendre compte du détail de sa réalisation plastique, que ce soit dans le Grand verre, dont les spécialistes d’histoire de l’art sont déjà nombreux à avoir démonté l’intrigante machinerie.3

Fiction transcendantale et fiction topologique

9Suivons pour commencer le fil de l’analogie avec la littérature de science-fiction, et plus particulièrement celle qui relève du genre « fiction topologique ». Si le thème de la pluralité des mondes, ou des mondes parallèles, y intervient parfois, c’est pour poser la question de la forme singulière d’un monde, et non, comme c’est le cas avec la fiction « transcendantale » illustrée par les romans de Philip K. Dick, celle de son unité, ni celle de la possibilité de faire-monde, de se rapporter ou de croire à un monde en général. Ici ce n’est pas le monde comme tel qui est en jeu, mais si l’on peut dire sa « tenue », son articulation dimensionnelle.

10La quatrième dimension est bien entendu le grand lieu commun de la fiction topologique.4 Il en est déjà question dans l’Homme invisible de H. G. Wells, mais aussi dans la nouvelle du même auteur intitulée « The Plattner Story » (1896). Robert Heinlein (« And he built a crooked house », 1940), Fritz Leiber (avec « Space-time for springers », 1958), et plus près de nous Greg Egan (« The infinite assassin », 1991), ont conçu sur ce thème des dimensions n de stimulantes variations. Cet intérêt constant de la science-fiction pour la quatrième dimension nous renvoie plus profondément à une affinité de la science-fiction avec la fiction mathématique. « Fiction mathématique » peut s’entendre au sens où un livre comme Flatland de Edwin A. Abbott propose une introduction pédagogique romancée à quelques idées géométriques élémentaires (et moins élémentaires), mais aussi bien au sens où des scientifiques comme Helmholtz ou Poincaré ont pu avoir recours, dans leurs œuvres « populaires », à des fictions imagées où des êtres « plats » (bidimensionnels) arpentent des surfaces courbes, où des mondes « non euclidiens » viennent prendre à contre-pied nos réflexes intuitifs.

11En somme, la science-fiction fictionne les mathématiques, parce que les mathématiques le font déjà elles-mêmes à travers les protocoles par lesquels elles cherchent à se faire entendre, au-delà de la cohérence déductive des preuves, en exhibant les objets et les opérations qui les occupent par le truchement de fictions porteuses d’intuition. Les mathématiques ne cessent de poser la question du caractère plus ou moins intuitionnable (ou plus ou moins constructible) de leurs concepts. Elles réclament, par exemple, des preuves de consistance qui passent en géométrie par la construction de modèles dans l’espace euclidien (pseudosphère de Beltrami, demi-disque de Poincaré). Quand il ne s’agit pas de donner une preuve formelle de la correspondance des axiomes et des théorèmes de deux géométries, on peut ressentir simplement le besoin d’éprouver certains concepts en donnant une démonstration intuitive de leur caractère opératoire. Ainsi, les diagrammes de Minkowski permettent-ils de ressaisir géométriquement les transformations de Lorentz en termes de rotations hyperboliques ; ils offrent surtout un support intuitif (un diagramme affiné, en l’occurrence) qui permet à l’esprit, oscillant d’une perspective à l’autre sans s’installer dans aucune, de s’acclimater à la manière dont le mouvement, si l’on peut dire, déforme l’espace : ainsi le temps s’unit à l’espace, se compose ou plutôt s’intrique en lui — au point qu’espace et temps en soi finissent par disparaître comme des ombres, pour reprendre la belle formule de Minkowski.

12Sans doute, toute élaboration d’une forme d’intuition (modèle, diagramme) n’est pas nécessairement une fiction. Mais elle y touche toujours par un bord. Il s’agit en effet de faire « comme si » : comme si nous étions des êtres plats, réduits à une perception bidimensionnelle, comme si nous étions capables de faire en quatre dimensions ce que nous savons faire dans le plan muni d’une métrique pseudo-euclidienne (dilater les durées, contracter les longueurs), etc. C’est là, en ce point où le calcul et la preuve se projettent sur des trames où l’imagination peut opérer à son aise, que la science-fiction se raccorde réellement à la science. C’est là qu’elle peut être autre chose qu’une méditation romancée sur les formes de l’imaginaire scientifique ou sur les fantasmes véhiculés par la technoscience.

Variations sur l’hypercube

13On pourrait se livrer, sur ce point, à une comparaison systématique des fictions qui mobilisent la figure de l’hypercube (soit un cube étalé en quatre dimensions). Ainsi, là où Wells, dans « The Plattner Story », cherche à rendre compte de l’hyperréalité à travers la collecte d’indices troublants (vieille idée de l’inversion des figures par retournement dans un espace de dimension quatre) ou, plus directement, à travers des descriptions à caractère hallucinatoire (celles auxquelles donnerait lieu une hypothétique vision en 4d), Heinlein, dans « And he built a crooked house », produit une description technique de l’hypercube en narrant les péripéties liées à l’exploration d’une architecture tridimensionnelle à la Escher, dont le principe d’organisation n’est pleinement compréhensible qu’à la condition d’être rapporté à un espace de dimension supérieure. Chaque pièce, chaque volume de cette maison n’est en réalité qu’une facette d’un hypervolume cubique en lui-même invisible. Les protagonistes de cette nouvelle ont affaire à un modèle tridimensionnel particulièrement intriqué de l’hypercube (le « tesseract »). L’auteur nous en livre le mode de construction à travers la voix d’un des personnages : il nous invite à imaginer, par analogie, que si le développement bidimensionnel d’un cube peut prendre la forme de six carrés assemblés en croix sur un plan (figure 1), huit cubes convenablement agencés peuvent fort bien constituer le développement en trois dimensions d’un hypercube dont les « faces » seraient, cette fois-ci, des volumes. Si la maison d’architecte apparaît biscornue, c’est que ses volumes sont déformés par les effets de perspective liés à la projection des figures quadridimensionnelles dans l’espace à trois dimensions.5 L’avantage d’une telle construction apparaît clairement une fois que l’on s’est familiarisé avec son étrange topologie. La maison tout entière peut reposer sur des fondations dont la surface n’excède pas celle d’une seule pièce, de sorte que chacune des huit « faces » cubiques donne sur l’extérieur, toutes les pièces offrant une vue sur le jardin. Les problèmes commencent, cependant, lorsque la maison, secouée par un tremblement de terre, se met soudain à bouger et finalement à se « replier » dans la quatrième dimension (ou, ce qui revient au même, à s’y redéployer sous sa forme quadridimensionnelle). La fiction nous invite alors à un saut imaginatif, suivant un rapport d’analogie 3d/4d : en suivant les protagonistes affolés qui courent d’une pièce à l’autre, elle suggère un parcours déroutant, littéralement désorienté, plein de rotations étranges et de raccourcis inattendus, sous l’hypothèse que la maison en trois dimensions n’était en fait qu’une version « dépliée » ou « projetée » de l’hyper-maison quadridimensionnelle à présent complètement formée. Mais une fois expliqué le principe géométrique de l’expérience, la fiction ne peut, bien entendu, pas faire mieux que donner de cet incident singulier des indices narratifs, en décrivant les effets de désorientation provoqués chez les personnages.

Figure 1 : Développement d’un cube (à droite) et d’un hypercube (à gauche).

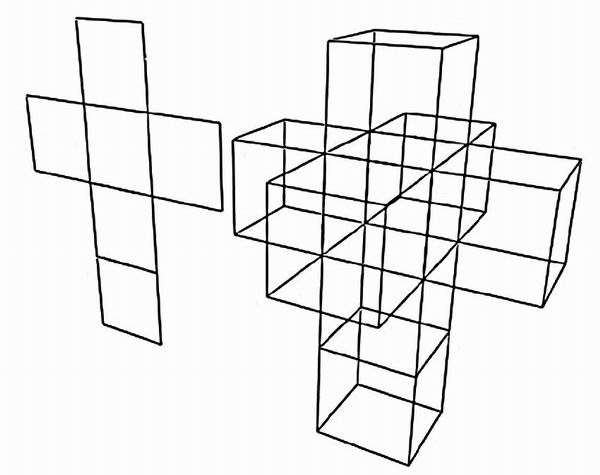
Figure 2 : Représentation d’un hypercube en perspective tridimensionnelle.

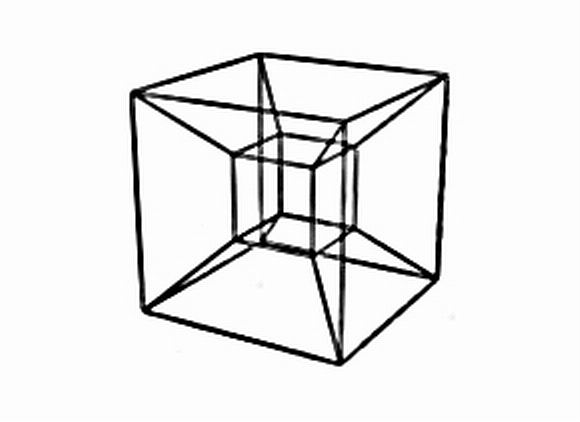
14Un pas supplémentaire est franchi avec une nouvelle de Greg Bear, auteur par ailleurs d’un chef-d’œuvre du genre « hard science », Eon. La nouvelle s’intitule « Tangents » (1986)6 : elle développe l’idée d’une exploration des virtualités quadridimensionnelles « tangentielles » strictement immanente aux trois dimensions d’espace habituelles. L’espace 4d (annoncé une fois de plus par la figure de l’hypercube) est figuré par des rotations dans l’espace à quatre dimensions, en elles-mêmes invisibles, mais dont on comprend qu’elles viennent recouper et parfois déchirer l’espace ordinaire, ou encore par des empreintes ou des moulages tridimensionnels d’objets quadridimensionnels, sortes d’ectoplasmes d’hyper-espace attirés par la musique d’un synthétiseur. Greg Bear place au cœur de son récit la problématique de la vision en quatre dimensions. Mais au lieu de nous en donner une sorte d’évocation suggestive et psychédélique, il insiste sur le difficile apprentissage de l’analogie, en donnant une place particulière à la notion de « direction » ouverte par la quatrième dimension de l’espace. Car on ne quitte pas l’analogie. Comme le dit l’un des protagoniste : « Our circuits are just too hard-wired, I suppose ». Nous sommes ainsi « câblés », c’est-à-dire formatés, conditionnés, pour penser en trois dimensions. Mais l’essentiel est d’essayer malgré tout, en se donnant des protocoles fictionnels. La fiction, une fois encore, fait comme si : comme s’il était possible de voir en quatre dimensions, à l’image de ce que nous faisons lorsque nous voyons en trois dimensions. Greg Bear parvient à en donner l’idée, illustrant ainsi le principe de toute fiction topologique : que tout groupe d’opérations mathématiques invoqué dans une fiction trouve sa contrepartie intuitive dans des gestes ou des formes directement opérables dans le cadre d’une narration possible.

L’intuition quadridimensionnelle : faux problèmes et vraies questions

15Grâce à ses installations, ses diagrammes et ses micro-récits, Duchamp entretient avec la science — celle du moins qui l’intéresse — un rapport du même genre. Ses excursions du côté de la géométrie, on l’a dit, ne relèvent pas d’une méditation ironique sur les lieux communs de la science du temps : il n’y a en ce sens nulle commune mesure entre les recherches duchampiennes sur les espaces à n dimensions et, par exemple, les références que peut faire un Dali à la relativité et aux espaces courbes, références qui ne se réduisent pas chez ce dernier au motif des montres molles, mais ne font jamais que prolonger, sur le mode de la surenchère, les débauches d’imagination auxquelles se livre la littérature de vulgarisation disponible à l’époque. L’intérêt de l’art-fiction est de chercher du côté des théories scientifiques des raccords opérant directement sur le terrain des questions formelles de l’art, plutôt que des métaphores fantastiques susceptibles de nourrir un discours parodique sur les transformations de la perception à l’âge des machines.  Revenons donc à la quatrième dimension et à sa mise en œuvre dans les notes du Grand verre. Cette tentative recoupe très directement les questions soulevées par les fictions topologiques. Elle y apporte même une réponse précise qui n’a pas — semble-t-il — d’équivalent dans le domaine littéraire. Ce que tente Duchamp, c’est en effet de fictionner la quatrième dimension sans recourir à l’analogie.

16Tout commence par un voyage mémorable : une automobile roulant à tombeau ouvert sur la route du Jura à Paris. Nous sommes en 1912. Dans cette voiture, se trouve Duchamp, en compagnie de Gabrielle Buffet, d’Apollinaire et de Picabia. De cette expérience cinétiquo-érotique où la puissance virginale de la Mariée (« l’automobiline, essence d’amour ») se conjugue avec le désir cylindré des célibataires (les « moteurs à explosion »), l’artiste tire l’exigence impérieuse d’une œuvre. Il faut en faire quelque chose. Cela le conduit au Grand verre, qu’il est juste d’aborder, dans un premier temps, comme la transposition plastique d’une expérience de pure vitesse. Voyage intensif, instantané et immobile, qui trouve son expression rigoureuse dans l’idée du déplacement invisible des formes dans un espace « sans orientation », mais à quatre dimensions — ou, ce qui revient au même, l’idée que les volumes visibles et tangibles qui forment l’enveloppe du Grand verre sont les projections de configurations invisibles déployées sur quatre dimensions. En effet, la vitesse pure, la vitesse infinie conquise au bout de cette route du Jura à Paris, réclamait quelque chose comme une abstraction d’espace. On ne pouvait plus se contenter de figurer la vitesse, comme faisaient les futuristes à la même époque, par des déplacements dans l’espace ordinaire, en le striant et en le saturant de lignes, ou bien en déformant les corps comme s’ils étaient soumis à des lignes de forces invisibles. Il fallait que la ligne soit autre chose qu’un tracé, ou une trajectoire. Il fallait qu’elle fende pour ainsi dire l’espace lui-même. D’où l’idée de l’engendrer activement à partir d’une fiction d’espace, au lieu de se donner l’espace tout fait pour le sillonner en tous sens.

« Graphiquement, cette route tendra vers la ligne pure géométrique sans épaisseur (la rencontre de deux plans me semble le seul moyen pictural d’arriver à la pureté.) »7

17Toute ligne peut en effet se signaler par le recoupement de deux surfaces invisibles qui se déplacent dans l’espace. Mais pourquoi s’arrêter en si bon chemin ? Duchamp va jusqu’au bout de sa pensée : de même que la ligne (espace à une dimension) peut être conçue comme le recoupement de deux surfaces, les surfaces et les volumes eux-mêmes peuvent être conçus comme les coupes ou les intersections d’espaces de dimensions supérieures qui pivoteraient pour ainsi dire sur eux-mêmes. Si bien que la Mariée tout entière, explique Duchamp, n’est rien d’autre que le résultat d’une projection à quatre dimensions dans notre monde à trois dimensions, projection elle-même re-projetée en deux dimensions sur le panneau transparent du Grand verre.8

18À la ligne de vitesse tracée par l’automobile répond donc un processus purement mental, dont le passage d’une dimension à l’autre doit donner l’équivalent projectif. Cependant, le Grand verre ne se contente pas d’étendre à la dimension quatre (c’est-à-dire au rapport entre les dimensions trois et quatre), par un simple transfert analogique, ce que la peinture n’a cessé de réinventer au cours de son histoire, à savoir la représentation bidimensionnelle des figures de l’espace à trois dimensions. Dans un premier temps, avec le Nu, Duchamp avait tenté d’échapper aux contraintes de la perspective classique en étalant les corps le long d’une quatrième dimension qui figurerait le temps : parfaite illustration du paradoxe bergsonien d’un mouvement recomposé par une succession d’arrêts (« mécanisme cinématographique »). Mais le désir de pure vitesse réclame tout autre chose : des « Rois et Reine traversés par des nus vites », par exemple — des nus qui zèbrent l’espace et le forcent d’une certaine manière à se mettre lui-même en mouvement, à devenir autre chose qu’un simple réceptacle ou milieu amorphe pour le mouvement des corps. Et cette exigence se traduit en pratique par une idée moins statique, plus constructive aussi, de la quatrième dimension. Car Duchamp n’est pas assez naïf pour donner dans le mysticisme ou le symbolisme des « n dimensions ». Il reconnaît d’emblée qu’il ne saurait être question de  saisir, dans un regard « hypervisuel », l’apparence « réelle » d’objets quadrimensionnels plongés dans un espace doté d’une dimension de plus que le nôtre. Tout le problème est en effet que le sens de l’expression « quatrième dimension » nous est irrémédiablement obscur tant qu’on s’imagine que l’analogie avec les dimensions inférieures peut nous donner accès à un équivalent de réalité, c’est-à-dire à un domaine ou un milieu qui aurait le même genre d’évidence que notre espace tridimensionnel.

« Objection : Quel est le sens de ce mot quatrièmedimension, puisqu’il n’a pas de correspondant tactile, ou sensoriel, comme ont la première, la seconde, la troisième dimension. »9 

19Le mieux que puisse faire l’analogie est donc de préparer l’esprit à un changement de régime opératoire : il ne s’agit plus alors de tenter de s’imaginer directement des objets singuliers, dotés d’une dimension supplémentaire, mais de comprendre, par exemple, que dans le continu quadrimensionnel

« le plan est toujours vu comme une ligne »,10

20et par conséquent, le volume comme une surface :

« L’objet 3 dimsl vu dans le continu 4 dimsl est perçu d’ensemble. »

21Comme chez Greg Bear, seule nous est donnée l’idée de ce qu’impliquerait une vision selon les quatre dimensions, par analogie avec ce que nous savons de ce que c’est que voir en trois dimensions. Il ne s’agit pas de chercher à développer l’intuition d’un objet quadridimensionnel, ni de dire seulement qu’un objet quadridimensionnel serait l’analogue d’un objet tridimensionnel vu simultanément sous toutes ses faces, mais de s’acclimater à l’idée de ce à quoi engagerait une perspective quadridimensionnelle.

22Le problème est que, si l’on n’a pas de mal à concevoir qu’une telle perspective nous donne les trois dimensions d’un seul coup, sous toutes ses faces, comme si elles se trouvaient dépliées et mises à plat (par analogie avec les surfaces, que nous embrassons d’un seul coup d’œil), on ne peut guère l’imaginer. Un tel objet « plat », pour nous, ne serait justement plus vraiment un objet, mais une simple surface. Notre expérience et notre idée de ce qu’est un objet impliquent essentiellement qu’il se tienne pour ainsi dire en réserve, qu’il ne se donne pas d’un seul coup et nous oblige à en faire le tour : c’est la sixième face du cube qui, en nous étant soustraite, témoigne par son absence de la profondeur et de la latence du visible. Qu’un objet quadridimensionnel se donne, lui aussi, par esquisses, et que ces esquisses prennent la forme de volumes « dépliés », nous pouvons bien le concevoir, mais cela ne nous donne toujours pas la moindre idée de ce à quoi ressemblerait un objet quadridimensionnel vu depuis la quatrième dimension. Et il n’est pas très utile, pour y parvenir, de s’efforcer de concevoir, par analogie, la manière dont un objet tridimensionnel se donnerait à un sujet à quatre dimensions : cette manœuvre nous ramène irrémédiablement à une vision sans profondeur, écrasée sur la surface plane d’une représentation purement mentale. Autant vaudrait chercher à se figurer la perception ordinaire des objets étalés en longueur, largeur et profondeur à partir de celle de créatures plates réduites à une vision bidimensionnelle.

23Il faut donc s’y résoudre : l’intuition ne peut franchir le seuil qui sépare la troisième dimension de la quatrième ; de l’une à l’autre, il y a toujours un saut. Mais la question, dira-t-on, est peut-être moins de savoir à quoi ressemblerait un volume vu en quatre dimensions, que de trouver les règles d’une représentation conforme d’une situation qui marque justement une limite de l’intuition. Duchamp revient donc à sa question :

« Quelle représentation peut-on donner d’un espace 3 dimsl dans un continu 4 dimsl ? »

24Le problème, ainsi formulé, n’est plus du tout celui de l’irreprésentable (l’hyper-objet 4d) ; le problème est celui de la figuration concrète de la limite comme telle, c’est-à-dire de l’articulation des dimensions (3d/4d). C’est à partir de cette question que Duchamp se met en quête d’une définition opératoire de la dimension, qui ne se contente pas de la situer aux confins de « l’art rétinien », comme une sorte de point de fuite imaginaire de la représentation perspective.

Le démon de l’analogie

25Aussi riche soit-elle par ailleurs en procédés représentatifs, la stratégie analogique finit par tourner court. Mais il n’est pas si facile de s’en débarrasser. L’analogisme agit en effet comme un véritable « obstacle épistémologique », parce qu’il ne peut construire son problème qu’à travers une accumulation de négations (ce que la quatrième dimension n’est pas, c’est ce qu’elle a de plus). Et Duchamp semble d’abord hésiter entre les deux stratégies, en somme assez classiques, que lui suggère cette voie négative. Il s’agit de la projection et du « parallélisme ».

26— 1. D’une part, donc, les projections : les volumes donnés en trois dimensions seront ressaisis comme des « sections » ou « intersections », des « coupes » ou facettes d’objets quadridimensionnels (fig. 3), mais aussi comme leurs « ombres portées » ou leurs empreintes (« moules mâlics »). C’est la quatrième dimension reconnue en creux, à travers ses profils. Ou, ce qui revient au même, c’est la quatrième dimension pensée comme totalisation de ces profils accumulés, à l’image de plans superposés qui recomposeraient un volume en même temps qu’ils le découperaient en tranches infinitésimales.11 On ne sort pas ici du dispositif phénoménologique ordinaire : on se contente de l’étendre, par analogie, à un espace qu’on suppose doté d’une profondeur supplémentaire. Et s’il est déjà question de coupes, il ne s’agit justement que de limites ou d’écrans interposés entre deux espaces de dimensions différentes :

un « solide à quatre dimensions sera limité par des volumes à trois dimensions / L’ombre portée d’une figure à quatre dimensions sur notre espace est une ombre à trois dimensions […] »12

Figure 3 : Le cube comme section dans un milieu quadridimensionnel

(dessin de Marcel Duchamp reproduit dans Duchamp du signe, op. cit., p. 126).

27— 2. La seconde classe de procédés, en apparence plus constructive, est en fait parfaitement complémentaire. Ces procédés se fondent sur le mouvement, c’est-à-dire l’engendrement actif d’une quatrième dimension par glissement, translation ou « parallélisme » le long d’une quatrième direction de l’espace (fig. 4), ou encore par rotation d’un volume en trois dimensions autour d’un plan ou d’une charnière invisible. Car

« on peut tourner autour de la figure 4 dimsl selon les quatre directions de l’étendue »,13

28et réciproquement, la figure peut tourner sur elle-même ou se déformer selon les quatre directions du continu à quatre dimensions — c’est même ce qui la définit comme quadridimensionnelle.

« Donc, un continu fini à trois dimensions est engendré par un continu fini à deux dimensions tournant (au sens général) autour d’une charnière finie à une dimension / Un continu fini à quatre dimensions est donc engendré par un continu fini à trois dimensions tournant (ici ce mot perd son sens physique. […]) autour d’une charnière finie à deux dimensions – / Une charnière à deux dimensions = surface infinie. »14

Figure 4 : Engendrement des directions successives par translation dans un espace de dimension supérieure ;

 dessin de Marcel Duchamp reproduit dans Duchamp du signe, op. cit., p. 138).

29L’inconvénient de ce « principe de charnière » tient, bien évidemment, à ce que le mot « tourner » perd dans ce cas tout sens physique et même intuitif,

« car il est évident, précise Duchamp, que si nous faisons tourner cette section plane sur un axe quelconque, nous n’engendrerons que des continus à 3 dim. »15

30 Par ailleurs, le procédé général du « parallélisme » qui permettrait d’obtenir un objet quadrimensionnel par analogie avec les engendrements successifs de la ligne par le point, du plan par la ligne et du volume par le plan, se trouve limité par le fait que nous ne savons pas — sinon, justement, par pure analogie — ce à quoi peut ressembler la translation d’un volume selon une direction perpendiculaire au trièdre de référence, qui permet ordinairement de repérer un espace à trois dimensions :

« ce parallélisme élémentaire exige en tant qu’opération géométrique une connaissance intuitive du continu à quatre dimensions »,16

31et c’est précisément cette connaissance intuitive qui nous fait défaut. En bref, la méthode du parallélisme suppose toujours un milieu où se font les mouvements. Il reste donc à « définir par connaissance intuitive la “direction” de cette quatrième dimension ». Ce qui nous renvoie, une fois de plus, aux procédés projectifs et aux aménagements de la perspective que commande le point de vue d’un « œil quadridimensionnel » : sections, coupes, etc.

32Sur ce point, Wittgenstein a bien saisi le nœud du problème posé par tous les modèles tridimensionnels ou bidimensionnels de l’hypercube. En un sens (analogique), il n’y a rien de plus simple que de se représenter un cube quadridimensionnel : on se donne une figure en trois dimensions (ou en deux), et on se dit que l’hypercube sera la même chose, mais dans un espace augmenté d’une dimension :

« etwas wie [ici Wittgenstein fait figurer le dessin d’un cube en perspective] nur mit 4 Ausdehnungen… »17 (« quelque chose comme ça, mais en quatre dimensions… »)

33Mais il y a là une espèce de mirage. Et celui qui nous soumettrait une figuration analogique de l’hypercube pourrait toujours s’entendre dire :

« [Tu me demandes] quel type d’image je recherche ? Certainement pas le cube quadridimensionnel tel que tu l’as dessiné [ici Wittgenstein fait référence à un hypercube dessiné en perspective, à la manière de la fig. 2]. Pour le moment, je n’ai, en fait d’image, que le mot, accompagné du refus de tout ce que tu pourras bien me montrer. »18

34Projection, coupes, empreintes, ou alors glissements et rotations. En pratique, les deux stratégies sont solidaires, puisqu’on procède dans les deux cas par extensions et par négations.

35Le modèle projectif est nécessairement additif : la perspective quadridimensionnelle, telle que nous la mettons en œuvre, procède toujours par extensions imaginaires — imaginaires, puisque de fait nous sommes incapables de pressentir directement ce que serait un point de vue quadridimensionnel, ou un mouvement selon la quatrième direction de l’espace. La quatrième dimension, c’est la troisième, plus le mouvement par lequel on lui adjoint quelque chose (une quatrième direction perpendiculaire aux trois autres). Wittgenstein n’y voit qu’un saut sur place : en réalité, on n’a jamais affaire qu’à la troisième dimension plus le mouvement par lequel je refuse comme insuffisante toute figuration tangible de la quatrième dimension. En sens inverse — mais c’est peut-être ce mouvement inverse qui livre la vérité du premier —, la troisième dimension n’est elle-même appréhendée que comme une quatrième dimension à laquelle manquerait quelque chose. Ainsi, les volumes ordinaires sont-ils de simples projections, sections ou profils d’« hypervolumes » quadridimensionnels. Au-delà du vice de circularité qui guette immanquablement ce type de caractérisation, l’omniprésence du modèle projectif montre bien qu’il ne s’agit jamais que de trouver une perspective élargie ou généralisée (« N’importe quelle forme est la perspective d’une autre forme selon certain point de fuite et certaine distance ») : continuer en somme à faire de la perspective, mais en entretenant la fiction (elle-même purement imaginaire, et peut-être pas assez façonnée, justement) d’une dimension ou d’un « degré de liberté » supplémentaire.

36D’autre part, le procédé additif est nécessairement négatif : sa manière de donner plus (une dimension n+1) consiste, on vient de le voir, à redéfinir la dimension familière (n) comme un reste : en somme, une dimension (n+1) – 1.

37L’idée de la dimension qui gouverne les stratégies projectives, avec tous les artifices qui devraient la rendre praticable (miroirs, charnières, etc.), est globalement analytique. C’est une autre manière de dire qu’elle procède par addition ou articulation : lié au mouvement, le nombre de dimensions indique les « degrés de liberté » dont on jouit pour se déplacer dans un espace (avant-arrière + gauche-droite + haut-bas, etc., ad infinitum). Mais ce nombre se confond le plus souvent avec le nombre de paramètres dont on a besoin pour repérer un point dans l'espace (x, y, z, etc.). Cette manière de présenter les choses aboutit à une version strictement analytique ou arithmétique de la dimension n.

38Or Duchamp cherche manifestement autre chose. Il veut sortir des impasses de l’« analogisme » — et des figures du désir qu’il ordonne – en inventant un procédé qui soit à la fois soustractif et positif. Et c’est Poincaré qui lui fournit la solution, en substituant à la définition analytique de la dimension une définition strictement topologique.

Changement de dimension : le procédé des coupures

39De fait, en un point critique des dernières notes de la « Boîte blanche », Duchamp transcrit presque littéralement un passage des Dernières pensées, publiées la même année que le voyage Jura-Paris. Voici ce qu’écrivait Poincaré :

 « Un continu a n dimensions quand on peut le décomposer en plusieurs parties en y pratiquant une ou plusieurs coupures, qui soient elles-mêmes des continus à n-1 dimensions. Le continu à n dimensions se trouve ainsi défini par le continu à n-1 dimensions ; c’est une définition par récurrence. »19

40Ainsi, la dimension n se trouve engendrée par récurrence, et non par analogie, justement. Le procédé est celui, purement soustractif, de la « coupure », qu’il ne faut pas confondre avec la coupe projective, même lorsqu’il arrive que les objets se confondent (car une coupure produit nécessairement une coupe, qui, d’un autre point de vue, peut se comprendre comme une projection).

41Le concept topologique de la dimension est lié à la possibilité de séparer un espace de lui-même, ou de le rendre non connexe. Un espace est connexe s’il est, pour faire bref, « d’un seul tenant ». Plus précisément : deux points d’une surface sont connectés, en dimension 2, s’ils peuvent être reliés par une ligne continue et totalement incluse dans la surface ;  la surface elle-même est dite connexe si deux de ses points quelconques sont connectés de cette manière. Le procédé des coupures revient donc à envisager la dimension d’un espace à partir de ses possibilités intrinsèques de déconnexion (coupes virtuelles). Il offre ainsi un accès plus intuitif et plus « intrinsèque » à la notion de dimension, puisqu’il l’appréhende pour ainsi dire du milieu même du continu à n dimension, au lieu d’envisager la situation « de haut » en tentant d’imaginer les mouvements d’objets (n-1)-dimensionnels dans un espace à n dimensions, ou encore en se donnant d’emblée trois échelons successifs (la dimension n, la dimension n-1, qui en est la projection, et la dimension n-2, qui permet d’enclencher le raisonnement analogique). Les coupures procèdent en somme de façon intrinsèque au lieu de procéder par échafaudages de dimensions et renvois incessants de l’une à l’autre (par projection ou déplacement virtuel).

42Ainsi, la définition, pour être soustractive, n’en est pas moins pleinement positive : elle nous place en effet d’emblée dans l’élément qui nous intéresse, celui d’un continu à quatre dimensions ; elle capture directement les propriétés internes de continuité et de connexité de cet espace. Si une part d’analogie intervient dans l’explication qui accompagne la définition, elle n’est en réalité qu’une béquille ; elle fait d’ailleurs porter l’attention moins sur des objets ou des formes intuitives que sur l’opération même de la coupure (coupure de la ligne ouverte par un point, de la ligne fermée par deux points, du plan par une ligne infinie, du volume par un plan infini, etc.). Nous ne pouvons certes rien imaginer de l’« hypervolume » tel qu’il s’offrirait, d’un seul tenant, à un œil quadridimensionnel. Mais nous pouvons du moins comprendre que pour le séparer en deux, il faudrait le couper à l’aide d’un volume en trois dimensions, qui serait alors la limite commune de ses parties disjointes (c’est en ce sens qu’on peut dire que le point de vue topologique « enveloppe » le point de vue perspectif). De ce geste, nous avons une intuition simple, qui renvoie à des opérations communes : le fil se rompt en un point, les ciseaux découpent la feuille de papier, le coup de hache fend la bûche en deux, etc.

43C’est pourquoi le procédé des coupures nous éloigne définitivement de tout mysticisme de la quatrième dimension : il ne s’agit plus de se prendre au vertige des négations, ni de multiplier les marques, symboles ou analogons d’entités invisibles étalées sur quatre dimensions, mais de susciter des « images virtuelles » à partir des opérations qui les rendent concevables. Déjà la « réalité » à trois dimensions est moins une chose qu’une loi d’engendrement valant pour une classe de figures, ou encore un ensemble de propriétés formelles invariantes par transformation.20 Pourquoi en irait-il autrement de la quatrième dimension ? Une « réalité » n’est rien d’autre qu’un « ensemble innombrable » d’« images virtuelles ». Et c’est quelques lignes après avoir noté que la définition topologique de la dimension, loin d’être « en défaut », confirme au contraire toutes ses recherches plastiques, que Duchamp finit par livrer la formule qui résume le mieux le problème autour duquel il n’a cessé de tourner. Cette formule prend à présent un peu plus de relief :

« Virtualité comme quatrième dimension : non pas la réalité sous l’apparence sensorielle, mais la représentation virtuelle d’un volume (analogue à sa réflexion dans un miroir). »21

44*

45La coupure tranche dans le virtuel. Elle permet d’envisager le continuum à n dimensions comme ce qui se laisse couper ou séparer de multiples façons, mais en affichant, chaque fois, le même type de consistance, les mêmes propriétés de continuité et de connexité. La science-fiction gagnerait à s’en inspirer pour imaginer de nouveaux récits. Sans doute, tout monde fictionnel est d’une certaine manière un monde parallèle ; mais les mondes dont s’occupe la science-fiction d’inspiration topologique seraient plutôt des mondes tangents ou perpendiculaires : non pas d’autres mondes possibles, mais des mondes à peine pensables, et dont il faut néanmoins reconnaître la nécessité dès lors qu’un monde est donné. Si ces mondes n’existent pas, ils insistent pour ainsi dire à la surface du nôtre, ou sur ses bords. Leur mode d’existence virtuel ne peut être avéré que par des procédés de coupures, dont il reste à inventer les équivalents narratifs. Ce n’est pas simple, car la coupure elle-même, saisie dans son acte, est peut-être au-delà de toute image. Telle est sans doute la leçon du Grand verre. « L’écart est une opération », écrit Duchamp. Mais comment montre-t-on, comment raconte-t-on une opération ?